「ラクな勉強方法ってないのか?」
誰もが考えたことがあると思います。
前の記事では「ラクな裏技なんてない」って言ってますが、中高生時代の私は常にラクな方法を模索していました。
正直な話、私自身はかなりの面倒くさがりです。
 塾長
塾長面倒だからこそ効率化!
今回はそんな私が実行していた以下の2つの方法論についてお話していきます。
- ラクな計算
- ラクな暗記
初めに言っておきますが、全然ラクじゃないです。逆に面倒くさいことをしています。
ただ、結果的に学力は付いたんじゃないかと思います。
ラクな計算
面倒くさがりの私は思いました。
「途中式や筆算をできるだけ書きたくない」
途中式も筆算もあまり書かない以上は、暗算で解いていくことになります。
ちなみに、そろばんとかを習っていた訳ではなく、素の計算力は高くないです。
結論から言うと、計算の工夫を極めました。
計算の工夫とは4×25=100などの答えが簡単になる計算を活用することです。小学校で少し習います。
こういった計算の工夫を利用し、計算の順序・約分のタイミングなどの計算過程を効率化していくのです。
例えば、24×25→6×4×25→6×100=600みたいな感じです。
こういった計算は小学校でも習っているのですが、使いこなしている生徒は少ないです。
ある程度経験を積んでいくと、暗算で処理できる計算の幅が広がっていきます。
あと、実は暗算をすることでワーキングメモリが鍛えられます。
ワーキングメモリは瞬間的な記憶領域のことです。ワーキングメモリが大きいほど、複雑な思考が可能になります。
私は面倒くさがりだった結果、気づかないうちにワーキングメモリを鍛えていたことになります。
ワーキングメモリについては以下参照。


じゃあ、とりあえず暗算すればよいのかという話になりますが、そんな単純ではありません。
正直、個人差があります。
速さと正確さのバランスが取れる範囲で、暗算に挑戦していくのが良いと思います。
途中式に関しては、ワーキングメモリの節約という捉え方もできます。
バランスよく途中式を書くことで、解くスピードが上がります。
ラクな暗記
面倒くさがりの私は思いました。
「暗記って面倒くさい」



ストレートすぎる…
だから考えました。
どーせ覚えるなら、最小限の暗記で最大限の成果を出したい。
その結果として、過程を理解することに特化しました。
基本的には何事にも『全体の流れ』『前後関係』が存在します。『なぜそうなるのか』という部分です。
その様なつながりを理解・暗記することに注力しました。理科や社会は教科書を繰り返し読んでいたような気がします。
このように過程を理解することで、予測・応用が利くようになります。
この流れなら多分こうなるよねって、テスト中に思いつくようになります。
私個人の体験としては、思ったよりも点数は取れてました。
応用問題が逆に得点できるという変な得点分布でした。
その反面、基礎の用語問題を落とすという『もったいない』得点分布でもありました。
一般的には、全体の流れを把握した後に、細かい詰めをしていくと思います。
私は詰めの部分で手を抜き、テスト本番でのひらめき勝負を仕掛けていた訳ですね。



絶対にまねしないように!
用語の暗記だけして全体を把握できていない生徒は割と多い気がします。
一つ一つの知識は覚えていますが、知識のつながりが意識できていないので、問題の出され方が変わると急にできなくなるタイプです。
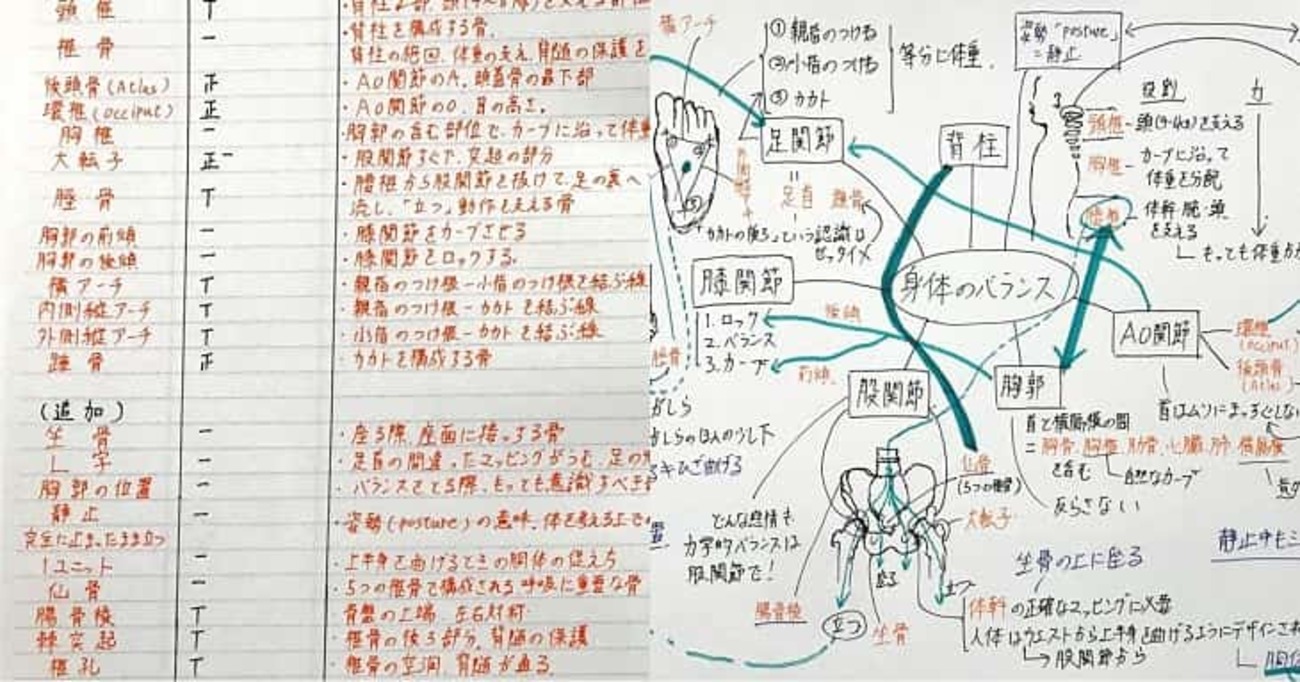
知識のつながりを自分で学ぶにはメモリーツリーが有効です。詳しくは以下参照。ついでに反復学習のコツも学べます。

ちなみに、このサイトはかなり優秀です。勉強関係の検索をするとかなりの確率で上位表示されます。
まとめ
「面倒くさい」と言って、逆に面倒くさい勉強方法をしていた中高生時代の私。
今になって思い返すと、意外と効果的な勉強をしていました。
「面倒」とは言いながらも「成果は出したい」という意識は謎に持っていたんですよね。
結果的に、効率的な勉強方法に仕上がっていったのかなと思います。



あと「努力量」の意識があればなぁ…
さて、現代では情報があふれかえっています。
今回のコラムで他サイトのリンクを埋め込んだように、探せば有用な情報はいくらでも出てきます。
しかし、情報はあっても自ら実行する人は少ないのが現状です。
それらの実行をサポートするのが、現代の塾の役目なのだろうかと考えています。



使える情報はいくらでも利用させてもらう!

